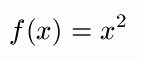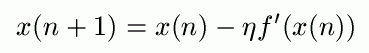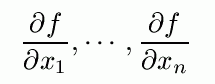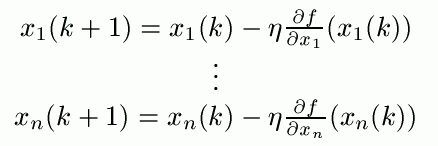Algorytm najszybszego spadku
Rozważmy następujący problem. Mamy daną pewną funkcję f i poszukujemy jej minimum startując od pewnego punktu x0. W tym ćwiczeniu przyjrzymy się jak dla tak sformułowanego zadania działa algorytm najszybszego spadku. Przyjmijmy, że funkcja f zdefiniowana jest następująco:
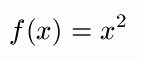
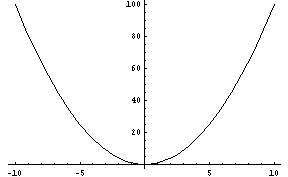
oraz jako stan startowy przyjmijmy x(0)=7.
Gdzie teraz poszukiwać minimum funkcji? Na lewo, czy na prawo od punktu x0?
Przypomnijmy sobie jakie informacje możemy uzyskać licząc pochodną funkcji. Jak wiadomo z analizy rzeczywistej, pochodna daje nam informacje na temat tego, czy funkcja jest rosnąca, czy malejąca. Jeśli przyjmuje ona wartości większe od zera w jakimś przedziale, to funkcja jest w nim rosnąca, jeśli mniejsze od zera - malejąca. Licząc w naszym przypadku wartość pochodnej w punkcie x0 otrzymujemy

Zatem funkcja jest rosnąca. Wynika stąd, że sensownie jest poruszać się w lewo od x0. O jaki krok? Zwykle przyjmuje się, że
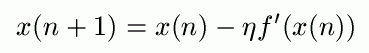
gdzie eta jest współczynnikiem regulującym wielkość kroku. Mówiąc precyzyjniej, będziemy się poruszać w kierunku ujemnego gradientu, który wyznacza nam kierunek najszybszego spadku wartości funkcji - stąd nazwa algorytmu: algorytm najszybszego spadku (czasem też algorytm najszybszego spadku gradientu).
Do tej pory wszystko jest chyba jasne i możemy mieć nadzieję, że algorytm rozwiąże postawiony na początku problem (znalezienie minimum funkcji). Niestety pojawiają się następujące komplikacje:
- Natrafienie na przedział, w którym funkcja jest stała, bądź też o bardzo małym nachyleniu. Wówczas pochodna jest równa dokładnie, lub też prawie, zero. To zaś oznacza, że

i utykamy w miejscu.
- Na ogół funkcje nie są takie ,,porządne'' jak rozważana w przykładzie funkcja i posiadają wiele minimów lokalnych. W takiej sytuacji algorytm po znalezieniu jednego z nich pozostanie w nim już na zawsze. Zatem moment, kiedy stwierdzimy, że kolejne iteracje nie dają zmiany w postaci nowych wartości x(n) może oznaczać, że znaleźliśmy poszukiwane minimum globalne, ale równie dobrze i niestety często tak właśnie jest, oznaczać to może, iż natrafiliśmy na płaski obszar lub też lokalne minimum.
- Dodatkowe utrudnienie stanowi warunek wymagajacy różniczkowalności funkcji.
Algorytm:
Załóżmy ogólnie, że mamy daną pewną funkcję f wielu zmiennych, której argument x jest postaci x=[x1,...,xn] oraz pewien punkt początkowy x(0)=[x(0)1,...,x(0)n], gdzie współrzędne wektorów x i x(0) mogą być dowolną liczną rzeczwyistą.
- k=0.
- Liczymy gradient:
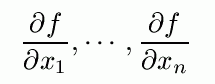
- Liczymy kolejny punkt w następujący sposób:
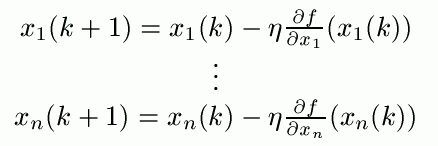
- Jeśli k < maxKroków, to zwiększ k o 1 i powróć do 2. W przeciwnym razie zakończ algorytm.
Rozwiązaniem pierwszego z zasygnalizowanych powyżej problemów może być bardzo prosta modyfikacja w właśnie przedstawionym algorytmie. Otóż obliczony w punkcie 3 gradient funkcji f wyznacza nam za każdym razem nowy kierunek, na którym należy poszukiwać minimum funkcji. Szczególnie dobrze bedzie to widoczne w przypadku funkcji dwóch zmienneych, co obrazują poniższe ilustracje. Im kolor na rysunku jest jaśniejszy, tym większą wartość w danym miejscu przyjmuje funkcja. Żółte ktopki to kolejne wartości x a czerwone linie wyznaczają drogę, po której przebiega minimalizacja.
![]()
Modyfikacja jest następująca. Za każdym razem, gdy wyznaczymy nowy kierunek poszukiwanie, czyli policzymy gradient, to nie robimy w tym kierunku kroku zależnego od eta, ale poszukujemy najmniejszej wartości na wyznaczonym kierunku. Odpowiadający jej argument będzie nowym x.
Sposobów na przeprowadzenie modyfikacji na wyznaczonym uprzedniu kierunku jest kilka, zwykle opierają się one na aproksymacji za pomocą wielomianu i poszukiwaniu minimu takiego wielomianu. Zdecydowanie najprostszy sposób przedstawić można w następujących krokach
Algorytm minimalizacji na zadanym kierunku:
- Rozpoczynamy obliczenia od pewnego wybranego pinktu xstart.
- Liczymy valurStart=f(xstart).
- Robimy malutki kroczek w wyznaczonym kierunku; niech na przykład kroczek=0.01*eta i otrzymujemy tym samym nowy punkt sstop.
- Liczymy valueStop=f(xstop).
- Jeśli valueStop > valueStart, czyli kolejny kroczek spowodował, że wartość funkcji wzrosła przyjmujemy, że xmin=xstart i kończymy procedure minimalizacji na zadanym kierunku.
W przeciwnym razie xstart=xstop i powracamy do 2.
Zatem robiąc dużo mniejsze kroczki niż wynikałoby to z wartości współczynnika eta posuwamy się w wyznaczonym kierunku tak długo dopóki wartości funkcji nie zaczną rosnąć. Jeśli za którymś razem nastąpi wzrost wartości, wówczas jako punkt minimalizujący przyjmujemy przedostatnio rozważany punkt. Z taką poprawką algorytm najszybszego spadku przyjmuje następującą postać
- k=0.
- Liczymy gradient:
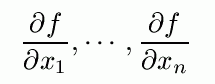
wyznaczający kierunek na którym należy poszukiwać minimum funkcji.
- Znajdź minimalną wartość na wyznaczonym kierunku według przedstawionego powyżej algorytmu. Argument, dla którego to minimum zostanie znalezione staje się nową wartościa x.
- Jeśli k < maxKroków, to zwiększ k o 1 i powróć do 2. W przeciwnym razie zakończ algorytm.
Warto (mam taką nadzieję) zapoznać się z następującym aplecikiem, na którym można troszeczkę bliżej przyjrzeć się działaniu algorytmu i jego modyfikacji.
Poniżej przedstawiam kilka rysunków pokazujących ścieżki powstałe w wyniku poszukiwania minimum w obu przypadkach.
![Różne ścieżki poszukiwania minimum]()
Zadanie:
Napisać programik podobny do tego z apleciku. Proszę sobie wybrać jakąś funkcję dwóch zmiennych według uznania. Dobrze jeśli program będzie graficznie pokazywał przebieg poszukiwania. Jeśli nie, to powinien wypisywać kolejne punkty x(k). Oczywiście programu musi pozwalać na podanie punktu startowego, wybranie kroku i metody (najszybszy spadek lub najszybszy spadek z minimalizają kierunkową).
|