Skip to content

Shamir’s Secret Sharing

In this part I cover the following topics


Protect an access to your data with password


Real life analogy

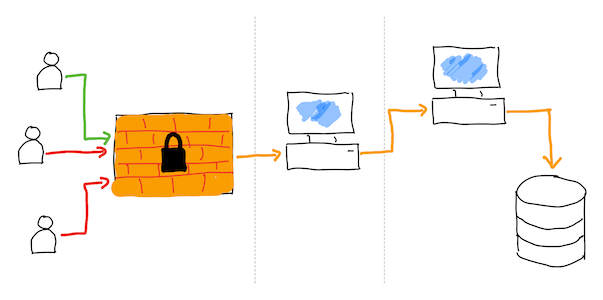
Keep secret things on the shelf and use padlock to lock door to your home.


Digital solution


How is it secure?

How is it secure? No to much. Saying the truth, not at all.

Breaking real life anlogy: break the window and enter the house. Now you have an access to everything which is inside.

Breaking digital solution: you don't have to break protection layer, which may be really hard to be chacked. Instead you can baypass it and get direct access to unprotected storage layer.

In our case, instead of using Python script, you can have a direct access to someone's secret. It's enough to know correct path which is much simpler to get than breaking password:


Protect your data with password

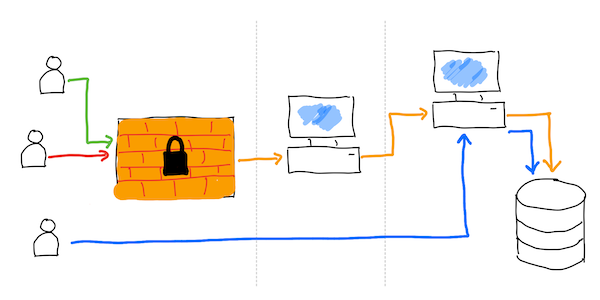
Now I change the scope: instead of protecting an access to your data with password I want you to protect your data itself.


Real life analogy

Use chest (box) and padlock to keep your private and secrete things hidden.


Digital solution

I use one-time pad (OTP) encryption technique to protect my data. For your information: this type of encryption cannot be broken. If you want to know more, read my article W poszukiwaniu szyfru idealnego.

Message:

Key:

Check files with message and key:

Encrypt message

Encrypted message

Decrypt message

Decrypted message:


What is wrong with this solution

The main problem with this case of encryption is related to key distribution procedure. Both sides, sender and recipient, must know the key used to transform a message (encrypt and decrypt). This problem is particularly acute in the case of the one-time pad ciphers, the length of which must not be less than the length of the encrypted message.


Protect your keys

The main question now is not if we can protect our data, but how we can protect our keys. Changing a little bit perspective, you may ask if there is a method to send secret data without sharing keys?


Real life analogy

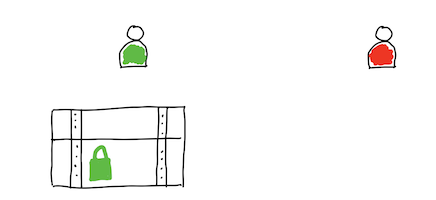
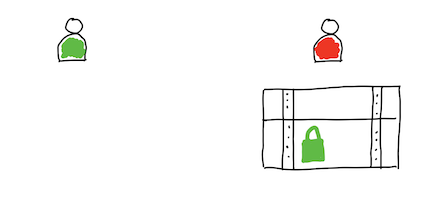
Use chest (box) and two padlocks to keep your private and secrete things hidden.












Digital solution

Use asymmetric public-key cryptography, known also as asymmetric cryptography. This is a cryptographic system that uses pairs of keys. Each pair consists of a public key (which may be known to others) and a private key (which may not be known by anyone except the owner).

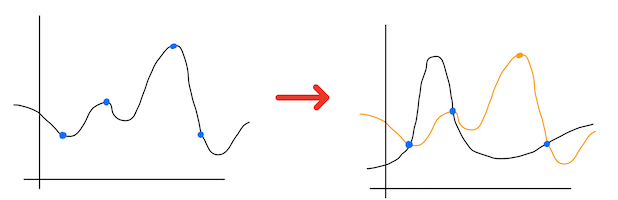
This type of crytpography is named asymmetric by contrasting it with one-key cryptography named symmetric. You can understand term (a)symmetricity looking into this image:

As you can see, in case of typical on-key cryptography, the same key is used to encrypt and decrypt message. When you draw a pipeline of steps needed to be performed during passing text which should be secret, you observe its symmetricity. In contrast, when you use pair of passwords, one is used to encrypt text while the second of them is used to decrypt message. You observe the asymmetry of the image.


Today ciphers are designed to withstand a wide range of attacks. An attacker should not be able to find the key, even if he knows any amount of plaintext and corresponding ciphertext. Modern encryption methods can be divided into the following categories:

Private-key cryptography (symmetric key algorithm): the same key is used for encryption and decryption.
Public-key cryptography (asymmetric key algorithm): two different keys are used for encryption and decryption.

Symmetric key ciphers can be divided into block ciphers and stream ciphers. Block ciphers operate on fixed-length groups of bits, called blocks, with an unvarying transformation. Stream ciphers encrypt plaintext digits one at a time on a continuous stream of data and the transformation of successive digits varies during the encryption process.


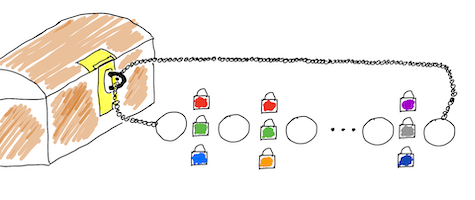
One more step further: protect your data with many passwords


Real life analogy

Imagine, you are a famous pirate. Over the years of your plundering activity, you have amassed a great deal of wealth. You want your treasures to be distributed among your five companions after your death. How to close the treasures in a chest so that none of your companions can open the chest by himself and take everything? You can use five padlocks. However, the profession of a pirate is not the most peaceful in the world. It is very likely that one of the five will die prematurely. So how to separate the keys so that one is not enough to open the chest, but it is enough to use any three of the five keys to open the lid of the chest?

You can do this, however it require you to consider all possible combinations (of 3-element subsets of a 5-element set):


To calculate the number of cases you can use a formula for combination. A combination is a selection of items from a set that has distinct members, such that the order of selection does not matter. More formally, a $k$-combination of a set $S$ is a subset of $k$ distinct elements of $S$. If the set has $n$ elements, the number of $k$-combinations, denoted as $C_{k}^{n}$, is equal to the binomial coefficient:
$${\binom {n}{k}}={\frac {n(n-1)\dotsb (n-k+1)}{k(k-1)\dotsb 1}} = \textstyle {\frac {n!}{k!(n-k)!}}$$,
whenever $k\leq n$.

In case of a 5-element set, you can create a 10 3-element subsets of it: 123, 124, 125, 134, 135, 145, 234, 235, 245, 345.


Digital solution

Another one analogy. You want to protect an access to nuclear missiles launch procedure. You don't want to let one madman, alone, launch the rockets on the launchers. So you distribute the access codes between several people. However, war is an extremely uncertain time and there is a good chance that several of them could die. So how do you make it possible to launch a rocket by specifying a minimum number of codes (greater than one), for example three out of five?

In digital word you can protect an access to nuclear missiles launch procedure writing code where you check all possible combinations:

With this code you can protect an access to your data but no data itself -- recall examples from the begining of this material: Protect an access to your data with password and Protect your data with password


Playing with simple geometry

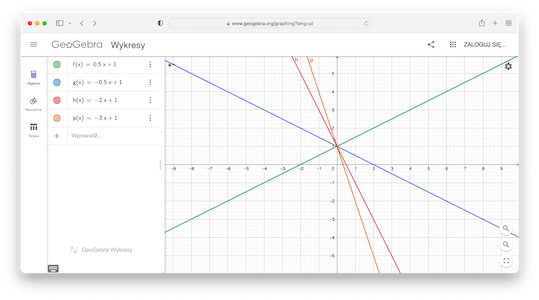
Even without deep mathematical background, it is quite easy to observe, that 2 points are sufficient to define a line.

If you have a line defined by some formula:
$$
f(x) = 0.5x+1
$$
it is very easy to find two distict point located on this line. Simply, select (randomly) two different numbers $x_1$ and $x_2$ and calculate corresponding values:
$$\begin{aligned}
&x_1 = -2 \\
&x_2 = 2\\
\end{aligned}$$

$$\begin{align}
& y_1 = f(x_1) = 0.5 (-2) + 1 = 0\\
& y_2 = f(x_2) = 0.5 \cdot 2 + 1 = 2\\
\end{align}$$

So you have two pairs of points belonging to this line:
$$\begin{align}
&p_1 = (x_1,y_1) = (-2,0)\\
&p_2 = (x_2,y_2) = (2,2)
\end{align}$$

You can repeat this procedure to obtain as many pairs of points as you want.

If you have two points you can easily find the equation of a line passes through thet two points:
$$\begin{align}
&q_1 = (x_3,y_3) = (0,1)\\
&q_2 = (x_4,y_4) = (1, 1.5)
\end{align}$$

$$\begin{align}
\frac{x-x_3}{x_3-x_4}
=
\frac{y-y_3}{y_3-y_4}
\end{align}$$

Doing simple transformations you can find the equation:
$$\begin{align}
\frac{x-0}{0-1}
=
\frac{y-1}{1-1.5}
\end{align}$$

$$\begin{align}
\frac{x}{-1}
=
\frac{y-1}{-0.5}
\end{align}$$

$$-x=\frac{y-1}{-0.5}$$

$$0.5x = y-1$$

$$y = 0.5x + 1$$

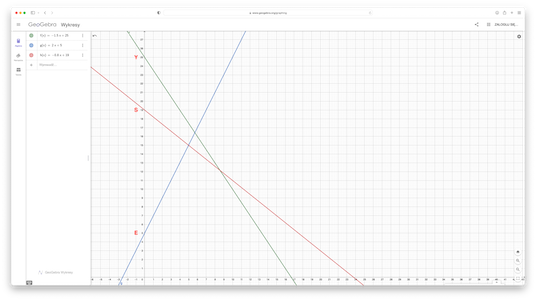
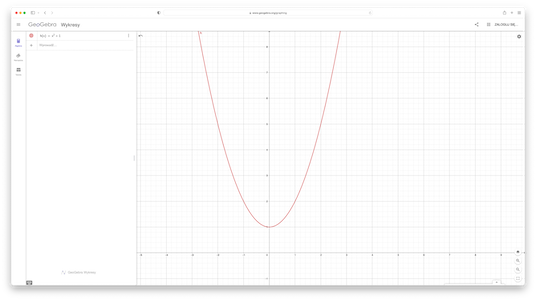
On the other hand, if you have only one point from this line, it is impossible to find thet line as there is infinitely many lines passing through this point (GeoGebra):


What is the point?

If you understand the concept of two points and line passes through them, you can use this concept to share some secret. How?

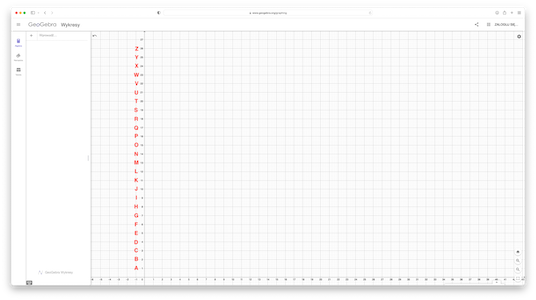
  1. First you have to place letters from alphabet on axis. To make it easier to plot, I put them on x-axis:

    According to the image, letter A is located at the point $p_A=(0,1)$, letter B at the point $p_B=(0,2)$ etc.

  2. Select a text you want to encrypt, for example: "YES".
  3. Next you have to select (randomly) three points (because text to encrypt has three characters). They can be any points you want, except points where first coordinate is equal to 0. I choose point $p_1 = (10,10)$, $p_2 = (6,17)$, $p_3 = (20,3)$.
  4. Find three equations of three lines (you can do this manually as you did before or use Python script from section Appendix: Line given by two points):
    • line $l_Y$ passes through point $p_1$ and $p_Y = (0, 25)$:

    • line $l_E$ passes through point $p_2$ and $p_E = (0, 5)$:

    • line $l_S$ passes through point $p_3$ and $p_S = (0, 19)$:

  5. On each line select (randomly) as many points as you have persons you want to share your secret message with. For example, if you decide to share secret with 4 person, you need four points on each line. These could be the following points:

    Line $l_1$ (1, 23.5) (3, 20.5) (5, 17.5) (7, 14.5)
    Line $l_2$ (1.5, 8.0) (4, 13) (6, 17) (8, 21)
    Line $l_3$ (2, 17.4) (3, 16.6) (5.5, 14.6) (6.7, 13.64)
  6. Points from column forms a data you have to pass to each person. So
    • Person One should obtain codes: (1, 23.5), (1.5, 8.0), (2, 17.4);
    • Person Two codes: (3, 20.5), (4, 13), (3, 16.6);
    • Person Three codes: (5, 17.5), (6, 17), (5.5, 14.6);
    • and Person Four codes: (7, 14.5), (8, 21), (6.7, 13.64).
    Person 1 Person 2 Person 3 Person 4
    Line $l_1$ (1, 23.5) (3, 20.5) (5, 17.5) (7, 14.5)
    Line $l_2$ (1.5, 8.0) (4, 13) (6, 17) (8, 21)
    Line $l_3$ (2, 17.4) (3, 16.6) (5.5, 14.6) (6.7, 13.64)

Because every two codes from sequence defines one point, every person knows position of three different points. However, no two points of them belong to the same line of $l_1$, $l_2$ and $l_3$. It is impossible for example for Person Two to find correct line equations. Second person, with its codes is needed. If Person Four joine to Person Two, than togethere thay can decrypt line equations. And having line, it is enough to get the x-axis crossing point and you will know corresponding letter.

Taking for example first pair from Person Two: (3, 20.5) and first pair from Person Four: (7, 14.5) you obtain equation:

whose graph intersects y-axis at the $p_Y = (25, 0)$ point which is what we expect.

If you take a first pair from Person Two: (3, 20.5) and first pair from Person Three: (5, 17.5) you the same equation:

whose graph intersects y-axis at the $p_Y = (25, 0)$ point which is what we expect.


Shamir's Secret Sharing

Now you are ready to hear about Shamir's Secret Sharing (SSS). This is a method used to secure a secret in a distributed way -- the secret is split into multiple parts, called shares. These shares are used to reconstruct the original secret. Each individual share is useless on its own but when all the shares are together, they reconstruct an original secret. Instead of all, Shamir’s scheme, requires a minimum number of shares (referred to as the threshold) needed to reconstruct the original secret.

You know, that this is possible when you use lines and points. With lines you have to use two shares to decrypt message. What if you require more shares to be used in order to recover message? Well, you can use generalization of line. Equation of a straight line is the simplest form of polynomial.

In mathematics, a polynomial is an expression consisting of indeterminates (more often called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables. An example of a polynomial of a single indeterminate $x$ is:
$$
x^2 − 4x + 7
$$
You can use polynomials to define functions:
$$
f(x) = x^2 − 4x + 7
$$
or... equation of a straight line:
$$
y= -1.5 x + 25.0
$$
or more generaly a curve:
$$
$$

A polynomial in a single indeterminate $x$ can always be written in the form:

$$a_{n}x^{n}+a_{n-1}x^{n-1}+\dotsb +a_{2}x^{2}+a_{1}x+a_{0}$$,

where $a_{0},\ldots ,a_{n}$ are constants and $x$ is the indeterminate. The highest of the degrees of the polynomial's monomials (individual terms) with non-zero coefficients is called the degree of a polynomial. The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non-negative integer. A polynomial function in one real variable can be represented by a graph.

So line is a specific case of polynomial:
$$a_{1}x+a_{0}$$
(compare with $y= -1.5 x + 25.0$).

It is proved that given $n+1$ pairs $(x_0,y_0),\dots,(x_n,y_n)$, with all the $x_i$, $i=0,\dots,n$ distinct, there is a unique polynomial $P(x)$ of degree (atmost) $n$ such that $P(x_i)=y_i$ for $i=0,\dots,n$. Other words, two points uniquely determine a degree 1 polynomial (a line), three points uniquely determine a degree 2 polynomial (quadratic function), four points uniquely determine a degree 3 polynomial, and so on.

You may ask, how do you determine the polynomial $P(x)=a_n x^n+\dots+a_1x+a_0$ such that $P(x_i) = y_i$ for $i = 0,\dots,n? There are two different simple and efficient algorithms for reconstructing the coefficients $a_0,...,a_n$, and therefore the polynomial $P(x)$.

In the first method, we write a system of $n + 1$ linear equations in $n + 1$ variables: the coefficients of the polynomial $a_0,...,a_n$. The $i$-th equation is:
$$
a_n x^n + a_{n-1}x^{n-1} +\dots+a_0 = y_i.
$$
Since $x_i$ and $y_i$ are constants, this is a linear equation in the $n+1$ unknowns $a_0,...,a_n$. Now solving these
equations gives the coefficients of the polynomial p(x).

For example, given the 3 pairs (−1,2), (0,1), and (2,5), you will construct the degree 2 polynomial $P(x)$` which goes through these points. The first equation says:
$$
a_2 (−1)^2 + a_1 (−1) + a_0 = 2
$$
Simplifying, you get:
$$
a_2 − a_1 + a_0 = 2.
$$
For the second and third equations, you get the following equations:
$$
a_2 (0)^2 + a_1 (0) + a_0 = 1
$$
simplified to:
$$
a_0 = 1
$$
and
$$
a_2 (2)^2 + a_1 (2) + a_0 = 5
$$
simplified to:
$$
4a_2 + 2a_1 + a_0 = 5.
$$
So, you obtain the following system of equations:
$$
\left\{
\begin{align}
&a_2 − a_1 + a_0 = 2\\
&a_0 = 1\\
&4a_2 + 2a_1 + a_0 = 5
\end{align}
\right.
$$
Now you should solve this system. In this case it is preety simple. Substituting for $a_0$ and multiplying the first equation by 2 you get:
$$\begin{eqnarray*}
2a_2 − 2a_1 &=& 2\\
4a_2 + 2a_1 &=& 4
\end{eqnarray*}$$
Then, adding down you find that $6a_2 = 6$, so $a_2 = 1$, and plugging back in you find that $a_1 = 0$. Thus, you have determined the polynomial:
$$
P(x) = x2 + 1
$$

Another worth to consider method is called Lagrange interpolation. The explanation how it works is not difficult, but nevertheless goes beyond the scope of this text. See Appendix: Lagrange interpolation for some details.

Above theorem holds when the values of the coefficients and the variable $x$ are chosen from the complex numbers instead of the real numbers or even the rational numbers. They do not hold if the values are restricted to being natural numbers or integers. Surprisingly, it holds when you are working over finite fields (Galois field). And this theory is behind real, applicable Shamir's Secret Sharing method.


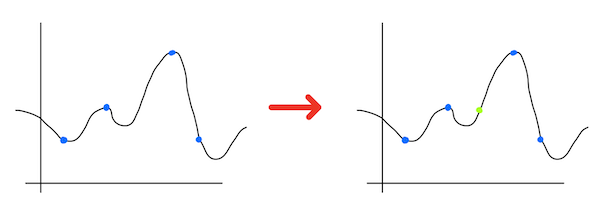
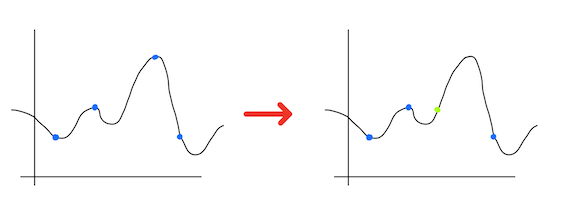
Properties of Shamir's Secret Sharing

One of the benefits of Shamir’s algorithm is that it is flexible and extensible. You can easily add, amend or remove shares at anytime you want to, without modifying the original secret.

Add share



Amend share



Remove share


Appendix


Appendix: Point on a line


Appendix: Line given by two points


Appendix: Lagrange interpolation

TODO